Reference
Quick Summary
These methods and properties you will probably use a lot:
|
Function minimizer and error computer. |
|
Run Migrad minimization. |
|
Run Hesse algorithm to compute asymptotic errors. |
|
Run Minos algorithm to compute confidence intervals. |
Access parameter values via an array-like view. |
|
Access parameter parabolic errors via an array-like view. |
|
Return a dict-like with Minos data objects. |
|
Access whether parameters are fixed via an array-like view. |
|
Access parameter limits via a array-like view. |
|
Return covariance matrix. |
|
Return True if the function minimum is valid. |
|
Return True if the covariance matrix is accurate. |
|
Get function value at minimum. |
|
Get number of fitted parameters (fixed parameters not counted). |
|
|
Get Minos profile over a specified interval. |
|
Get 2D Minos confidence region. |
|
Visualize agreement of current model with data (requires matplotlib). |
|
Draw matrix of Minos scans (requires matplotlib). |
Main interface
- class iminuit.Minuit(fcn: Cost, *args: float | ArrayLike, grad: CostVector | bool | None = None, g2: CostVector | bool | None = None, hessian: CostVector | bool | None = None, name: Collection[str] | None = None, **kwds: float)
Function minimizer and error computer.
Initialize Minuit object.
This does not start the minimization or perform any other work yet. Algorithms are started by calling the corresponding methods.
- Parameters:
fcn – Function to minimize. See notes for details on what kind of functions are accepted.
*args – Starting values for the minimization as positional arguments. See notes for details on how to set starting values.
grad (callable, bool, or None, optional) – If grad is a callable, it must be a function that calculates the gradient and returns an iterable object with one entry for each parameter, which is the derivative of fcn for that parameter. If None (default), Minuit will call the function
iminuit.util.gradient()on fcn. If this function returns a callable, it will be used, otherwise Minuit will internally compute the gradient numerically. Please see the documentation ofiminuit.util.gradient()how gradients are detected. Passing a boolean override this detection. If grad=True is used, a ValueError is raised if no useable gradient is found. If grad=False, Minuit will internally compute the gradient numerically.g2 (callable, bool, or None, optional) – Analog to grad, but computes G2, the diagonal of the hessian matrix. If None (default), Minuit will call the function
iminuit.util.g2()on fcn.hessian (callable, bool, or None, optional) – Analog to grad, but computes the Hessian matrix. The Hessian matrix must be a square symmetric matrix. Returning numpy arrays is the most efficient way, but any array-like works. If None (default), Minuit will call the function
iminuit.util.hessian()on fcn.name (sequence of str, optional) – If it is set, it overrides iminuit’s function signature detection.
**kwds – Starting values for the minimization as keyword arguments. See notes for details on how to set starting values.
Notes
Callables
By default, Minuit assumes that the callable fcn behaves like chi-square function, meaning that the function minimum in repeated identical random experiments is chi-square distributed up to an arbitrary additive constant. This is important for the correct error calculation. If fcn returns a log-likelihood, one should multiply the result with -2 to adapt it. If the function returns the negated log-likelihood, one can alternatively set the attribute fcn.errordef =
Minuit.LIKELIHOODorMinuit.errordef=Minuit.LIKELIHOODafter initialization to make Minuit calculate errors properly.Minuit reads the function signature of fcn to detect the number and names of the function parameters. Two kinds of function signatures are understood.
Function with positional arguments.
The function has positional arguments, one for each fit parameter. Example:
def fcn(a, b, c): ...
The parameters a, b, c must accept a real number.
iminuit automatically detects the parameters names in this case. More information about how the function signature is detected can be found in
iminuit.util.describe().Function with arguments passed as a single Numpy array.
The function has a single argument which is a Numpy array. Example:
def fcn_np(x): ...
To use this form, starting values need to be passed to Minuit in form as an array-like type, e.g. a numpy array, tuple or list. For more details, see “Parameter Keyword Arguments” further down.
In some cases, the detection fails, for example, for a function like this:
def difficult_fcn(*args): ...
To use such a function, set the name keyword as described further below.
Parameter initialization
Initial values for the minimization can be set with positional arguments or via keywords. This is best explained through an example:
def fcn(x, y): return (x - 2) ** 2 + (y - 3) ** 2
The following ways of passing starting values are equivalent:
Minuit(fcn, x=1, y=2) Minuit(fcn, y=2, x=1) # order is irrelevant when keywords are used ... Minuit(fcn, 1, 2) # ... but here the order matters
Positional arguments can also be used if the function has no signature:
def fcn_no_sig(*args): # ... Minuit(fcn_no_sig, 1, 2)
If the arguments are explicitly named with the name keyword described further below, keywords can be used for initialization:
Minuit(fcn_no_sig, x=1, y=2, name=("x", "y")) # this also works
If the function accepts a single Numpy array, then the initial values must be passed as a single array-like object:
def fcn_np(x): return (x[0] - 2) ** 2 + (x[1] - 3) ** 2 Minuit(fcn_np, (1, 2))
Setting the values with keywords is not possible in this case. Minuit deduces the number of parameters from the length of the initialization sequence.
- contour(x: int | str, y: int | str, *, size: int = 50, bound: float | Iterable[Tuple[float, float]] = 2, grid: Tuple[ArrayLike, ArrayLike] = None, subtract_min: bool = False) Tuple[ndarray, ndarray, ndarray]
Get a 2D contour of the function around the minimum.
It computes the contour via a function scan over two parameters, while keeping all other parameters fixed. The related
mncontour()works differently: for each pair of parameter values in the scan, it minimises the function with the respect to all other parameters.This method is useful to inspect the function near the minimum to detect issues (the contours should look smooth). It is not a confidence region unless the function only has two parameters. Use
mncontour()to compute confidence regions.- Parameters:
x (int or str) – First parameter for scan.
y (int or str) – Second parameter for scan.
size (int or tuple of int, optional) – Number of scanning points per parameter (Default: 50). A tuple is interpreted as the number of scanning points per parameter. Ignored if grid is set.
bound (float or tuple of floats, optional) – If bound is 2x2 array, [[v1min,v1max],[v2min,v2max]]. If bound is a number, it specifies how many \(\sigma\) symmetrically from minimum (minimum+- bound*:math:sigma). (Default: 2). Ignored if grid is set.
grid (tuple of array-like, optional) – Grid points to scan over. If grid is set, size and bound are ignored.
subtract_min – Subtract minimum from return values (Default: False).
- Returns:
array of float – Parameter values of first parameter.
array of float – Parameter values of second parameter.
2D array of float – Function values.
- draw_contour(x: int | str, y: int | str, **kwargs) Tuple[ndarray, ndarray, ndarray]
Draw 2D contour around minimum (requires matplotlib).
See
contour()for details on parameters and interpretation. Please also read the docs ofmncontour()to understand the difference between the two.See also
- draw_mncontour(x: int | str, y: int | str, *, cl: float | ArrayLike = None, size: int = 100, interpolated: int = 0, experimental: bool = False) Any
Draw 2D Minos confidence region (requires matplotlib).
See
mncontour()for details on the interpretation of the region and for the parameters accepted by this function.Examples
from iminuit import Minuit def cost(x, y, z): return (x - 1) ** 2 + (y - x) ** 2 + (z - 2) ** 2 cost.errordef = Minuit.LEAST_SQUARES m = Minuit(cost, x=0, y=0, z=0) m.migrad() m.draw_mncontour("x", "y")
(
Source code,png,hires.png,pdf)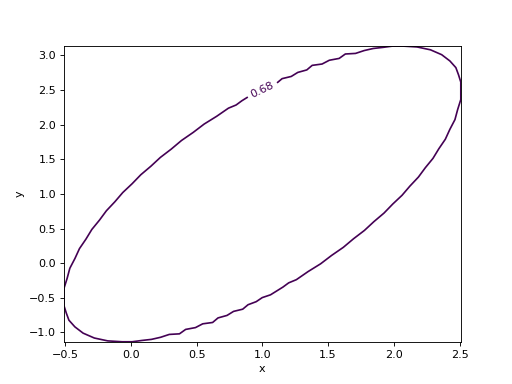
- Returns:
Instance of a ContourSet class from matplot.contour.
- Return type:
ContourSet
See also
- draw_mnmatrix(*, cl: float | ArrayLike = None, size: int = 100, experimental: bool = False, figsize=None) Any
Draw matrix of Minos scans (requires matplotlib).
This draws a matrix of Minos likelihood scans, meaning that the likelihood is minimized with respect to the parameters that are not scanned over. The diagonal cells of the matrix show the 1D scan, the off-diagonal cells show 2D scans for all unique pairs of parameters.
The projected edges of the 2D contours do not align with the 1D intervals, because of Wilks’ theorem. The levels for 2D confidence regions are higher. For more information on the interpretation of 2D confidence regions, see
mncontour().- Parameters:
cl (float or array-like of floats, optional) – See
mncontour().size (int, optional) – See
mncontour()experimental (bool, optional) – See
mncontour()figsize ((float, float) or None, optional) – Width and height of figure in inches.
Examples
from iminuit import Minuit def cost(a, b, c): return ( a**2 + 0.25 * a**4 + a * b + ((b - 1) / 0.6) ** 2 - 2.5 * b * c + ((c - 2) / 0.5) ** 2 ) m = Minuit(cost, 1, 1, 1) m.migrad() m.draw_mnmatrix(cl=[1, 2, 3])
(
Source code,png,hires.png,pdf)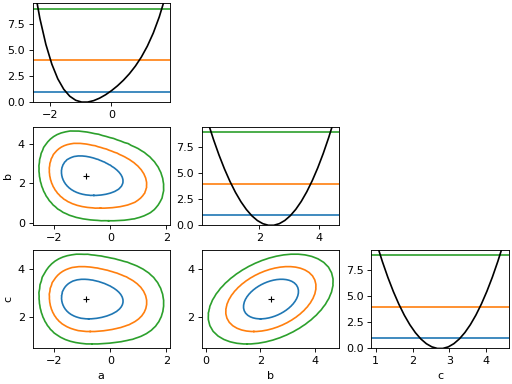
- Returns:
Figure and axes instances generated by matplotlib.
- Return type:
fig, ax
See also
mncontour,mnprofile,draw_mncontour,draw_contour,draw_profile
- draw_mnprofile(vname: int | str, *, band: bool = True, text: bool = True, **kwargs) Tuple[ndarray, ndarray]
Draw Minos profile over a specified interval (requires matplotlib).
See
mnprofile()for details and shared arguments. The following additional arguments are accepted.- Parameters:
vname (int or string) – Which variable to scan over, can be identified by index or name.
band (bool, optional) – If true, show a band to indicate the Hesse error interval (Default: True).
text (bool, optional) – If true, show text a title with the function value and the Hesse error (Default: True).
**kwargs – Other keyword arguments are forwarded to
mnprofile().
Examples
from iminuit import Minuit def cost(x, y, z): return (x - 1) ** 2 + (y - x) ** 2 + (z - 2) ** 2 cost.errordef = Minuit.LEAST_SQUARES m = Minuit(cost, x=0, y=0, z=0) m.migrad() m.draw_mnprofile("y")
(
Source code,png,hires.png,pdf)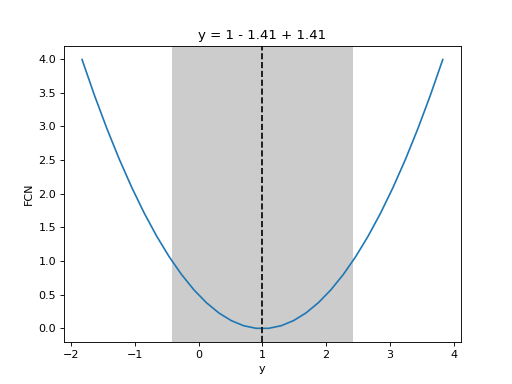
See also
- draw_profile(vname: int | str, *, band: bool = True, text: bool = True, **kwargs) Tuple[ndarray, ndarray]
Draw 1D cost function profile over a range (requires matplotlib).
See
profile()for details and shared arguments. The following additional arguments are accepted.- Parameters:
band (bool, optional) – If true, show a band to indicate the Hesse error interval (Default: True).
text (bool, optional) – If true, show text a title with the function value and the Hesse error (Default: True).
See also
profile,draw_mnprofile,draw_contour,draw_mncontourprofile
- fixto(key: int | str | slice | List[str | int], value: float | Iterable[float]) Minuit
Fix parameter and set it to value.
This is a convenience function to fix a parameter and set it to a value at the same time. It is equivalent to calling
fixedandvalues.- Parameters:
key (int, str, slice, list of int or str) – Key, which can be an index, name, slice, or list of indices or names.
value (float or sequence of float) – Value(s) assigned to key(s).
- Return type:
self
- hesse(ncall: int | None = None) Minuit
Run Hesse algorithm to compute asymptotic errors.
The Hesse method estimates the covariance matrix by inverting the matrix of second derivatives (Hesse matrix) at the minimum. To get parameters correlations, you need to use this. The Minos algorithm is another way to estimate parameter uncertainties, see
minos().- Parameters:
ncall – Approximate upper limit for the number of calls made by the Hesse algorithm. If set to None, use the adaptive heuristic from the Minuit2 library (Default: None).
Notes
The covariance matrix is asymptotically (in large samples) valid. By valid we mean that confidence intervals constructed from the errors contain the true value with a well-known coverage probability (68 % for each interval). In finite samples, this is likely to be true if your cost function looks like a hyperparabola around the minimum.
In practice, the errors very likely have correct coverage if the results from Minos and Hesse methods agree. It is possible to construct artifical functions where this rule is violated, but in practice it should always work.
See also
- interactive(plot: Callable = None, raise_on_exception=False, **kwargs)
Interactive GUI for fitting.
Starts a fitting application (requires PySide6, matplotlib) in which the fit is visualized and the parameters can be manipulated to find good starting parameters and to debug the fit.
When called in a Jupyter notebook (requires ipywidgets, IPython, matplotlib), a fitting widget is returned instead, which can be displayed.
- Parameters:
plot (Callable, optional) – To visualize the fit, interactive tries to access the visualize method on the cost function, which accepts the current model parameters as an array-like and potentially further keyword arguments, and draws a visualization into the current matplotlib axes. If the cost function does not provide a visualize method or if you want to override it, pass the function here.
raise_on_exception (bool, optional) – The default is to catch exceptions in the plot function and convert them into a plotted message. In unit tests, raise_on_exception should be set to True to allow detecting errors.
**kwargs – Any other keyword arguments are forwarded to the plot function.
Examples
from iminuit import Minuit, cost import numpy as np from matplotlib import pyplot as plt # custom visualization; x, y, model are taken from outer scope def viz(args): plt.plot(x, y, "ok") xm = np.linspace(x[0], x[-1], 100) plt.plot(xm, model(xm, *args)) def model(x, a, b): return a + b * x x = np.array([1, 2, 3, 4, 5]) y = np.array([1.03, 1.58, 2.03, 2.37, 3.09]) c = cost.LeastSquares(x, y, 0.1, model) m = Minuit(c, 0.5, 0.5) m.interactive(viz) # m.interactive() also works and calls LeastSquares.visualize
See also
- migrad(ncall: int | None = None, iterate: int = 5, use_simplex: bool = True) Minuit
Run Migrad minimization.
Migrad from the Minuit2 library is a robust minimisation algorithm which earned its reputation in 40+ years of almost exclusive usage in high-energy physics. How Migrad works is described in the Minuit paper. It uses first and approximate second derivatives to achieve quadratic convergence near the minimum.
- Parameters:
ncall (int or None, optional) – Approximate maximum number of calls before minimization will be aborted. If set to None, use the adaptive heuristic from the Minuit2 library (Default: None). Note: The limit may be slightly violated, because the condition is checked only after a full iteration of the algorithm, which usually performs several function calls.
iterate (int, optional) – Automatically call Migrad up to N times if convergence was not reached (Default: 5). This simple heuristic makes Migrad converge more often even if the numerical precision of the cost function is low. Setting this to 1 disables the feature.
use_simplex (bool, optional) – If we have to iterate, set this to True to call the Simplex algorithm before each call to Migrad (Default: True). This may improve convergence in pathological cases (which we are in when we have to iterate).
- minos(*parameters: int | str, cl: float = None, ncall: int | None = None) Minuit
Run Minos algorithm to compute confidence intervals.
The Minos algorithm uses the profile likelihood method to compute (generally asymmetric) confidence intervals. It scans the negative log-likelihood or (equivalently) the least-squares cost function around the minimum to construct a confidence interval.
- Parameters:
*parameters – Names of parameters to generate Minos errors for. If no positional arguments are given, Minos is run for each parameter.
cl (float or None, optional) – Confidence level of the interval. If not set or None, a standard interval is computed (default). A standard interval has about 68.3 % confidence, which is the probability of being within one standard deviation around the mean of a normal distribution. If 0 < cl < 1, the value is interpreted as the confidence level (a probability). For convenience, values cl >= 1 are interpreted as the probability content of a central symmetric interval covering that many standard deviations of a normal distribution. For example, cl=1 is interpreted as about 68.3 %, and cl=2 as 84.3 %, and so on. Using values other than 0.68, 0.9, 0.95, 0.99, 1, 2, 3, 4, 5 require the scipy module.
ncall (int or None, optional) – Limit the number of calls made by Minos. If None, an adaptive internal heuristic of the Minuit2 library is used (Default: None).
Notes
Asymptotically (large samples), the Minos interval has a coverage probability equal to the given confidence level. The coverage probability is the probability for the interval to contain the true value in repeated identical experiments.
The interval is invariant to transformations and thus not distorted by parameter limits, unless the limits intersect with the confidence interval. As a rule-of-thumb: when the confidence intervals computed with the Hesse and Minos algorithms differ strongly, the Minos intervals are preferred. Otherwise, Hesse intervals are preferred.
Running Minos is computationally expensive when there are many fit parameters. Effectively, it scans over one parameter in small steps and runs a full minimisation for all other parameters of the cost function for each scan point. This requires many more function evaluations than running the Hesse algorithm.
- mncontour(x: int | str, y: int | str, *, cl: float = None, size: int = 100, interpolated: int = 0, experimental: bool = False, ncall: int = 0, iterate: int = 5, use_simplex: bool = True) ndarray
Get 2D Minos confidence region.
This scans over two parameters and minimises all other free parameters for each scan point. This scan produces a statistical confidence region according to the profile likelihood method with a confidence level cl, which is asymptotically equal to the coverage probability of the confidence region according to Wilks’ theorem <https://en.wikipedia.org/wiki/Wilks%27_theorem>. Note that 1D projections of the 2D confidence region are larger than 1D Minos intervals computed for the same confidence level. This is not an error, but a consequence of Wilks’ theorem.
The calculation is expensive since a numerical minimisation has to be performed at various points.
- Parameters:
x (str) – Variable name of the first parameter.
y (str) – Variable name of the second parameter.
cl (float or None, optional) – Confidence level of the contour. If not set or None, a standard 68 % contour is computed (default). If 0 < cl < 1, the value is interpreted as the confidence level (a probability). For convenience, values cl >= 1 are interpreted as the probability content of a central symmetric interval covering that many standard deviations of a normal distribution. For example, cl=1 is interpreted as 68.3 %, and cl=2 is 84.3 %, and so on. Using values other than 0.68, 0.9, 0.95, 0.99, 1, 2, 3, 4, 5 require the scipy module.
size (int, optional) – Number of points on the contour to find (default: 100). Increasing this makes the contour smoother, but requires more computation time.
interpolated (int, optional) – Number of interpolated points on the contour (default: 0). If you set this to a value larger than size, cubic spline interpolation is used to generate a smoother curve and the interpolated coordinates are returned. Values smaller than size are ignored. Good results can be obtained with size=20, interpolated=200. This requires scipy.
experimental (bool, optional) – If true, use experimental implementation to compute contour, otherwise use MnContour from the Minuit2 library. The experimental implementation was found to succeed in cases where MnContour produced no reasonable result, but is slower and not yet well tested in practice. Use with caution and report back any issues via Github.
ncall (int, optional) – This parameter only takes effect if
experimentalis True. Approximate maximum number of calls before minimization will be aborted. If set to 0, use the adaptive heuristic from the Minuit2 library (Default: 0).iterate (int, optional) – This parameter only takes effect if
experimentalis True. Automatically call Migrad up to N times if convergence was not reached (Default: 5). This simple heuristic makes Migrad converge more often even if the numerical precision of the cost function is low. Setting this to 1 disables the feature.use_simplex (bool, optional) – This parameter only takes effect if
experimentalis True. If we have to iterate, set this to True to call the Simplex algorithm before each call to Migrad (Default: True). This may improve convergence in pathological cases (which we are in when we have to iterate).
- Returns:
Contour points of the form [[x1, y1]…[xn, yn]]. Note that N = size + 1, the last point [xn, yn] is identical to [x1, y1]. This makes it easier to draw a closed contour.
- Return type:
array of float (N x 2)
- mnprofile(vname: int | str, *, size: int = 30, bound: float | UserBound = 2, grid: ArrayLike = None, subtract_min: bool = False, ncall: int = 0, iterate: int = 5, use_simplex: bool = True) Tuple[ndarray, ndarray, ndarray]
Get Minos profile over a specified interval.
Scans over one parameter and minimises the function with respect to all other parameters for each scan point.
- Parameters:
vname (int or str) – Parameter to scan over.
size (int, optional) – Number of scanning points (Default: 100). Ignored if grid is set.
bound (tuple of float or float, optional) – If bound is tuple, (left, right) scanning bound. If bound is a number, it specifies an interval of N \(\sigma\) symmetrically around the minimum (Default: 2). Ignored if grid is set.
grid (array-like, optional) – Parameter values on which to compute the profile. If grid is set, size and bound are ignored.
subtract_min (bool, optional) – If true, subtract offset so that smallest value is zero (Default: False).
ncall (int, optional) – Approximate maximum number of calls before minimization will be aborted. If set to 0, use the adaptive heuristic from the Minuit2 library (Default: 0). Note: The limit may be slightly violated, because the condition is checked only after a full iteration of the algorithm, which usually performs several function calls.
iterate (int, optional) – Automatically call Migrad up to N times if convergence was not reached (Default: 5). This simple heuristic makes Migrad converge more often even if the numerical precision of the cost function is low. Setting this to 1 disables the feature.
use_simplex (bool, optional) – If we have to iterate, set this to True to call the Simplex algorithm before each call to Migrad (Default: True). This may improve convergence in pathological cases (which we are in when we have to iterate).
- Returns:
array of float – Parameter values where the profile was computed.
array of float – Profile values.
array of bool – Whether minimisation in each point succeeded or not.
- profile(vname: int | str, *, size: int = 100, bound: float | UserBound = 2, grid: ArrayLike = None, subtract_min: bool = False) Tuple[ndarray, ndarray]
Calculate 1D cost function profile over a range.
A 1D scan of the cost function around the minimum, useful to inspect the minimum. For a fit with several free parameters this is not the same as the Minos profile computed by
mncontour().- Parameters:
vname (int or str) – Parameter to scan over.
size (int, optional) – Number of scanning points (Default: 100). Ignored if grid is set.
bound (tuple of float or float, optional) – If bound is tuple, (left, right) scanning bound. If bound is a number, it specifies an interval of N \(\sigma\) symmetrically around the minimum (Default: 2). Ignored if grid is set.
grid (array-like, optional) – Parameter values on which to compute the profile. If grid is set, size and bound are ignored.
subtract_min (bool, optional) – If true, subtract offset so that smallest value is zero (Default: False).
- Returns:
array of float – Parameter values.
array of float – Function values.
- reset() Minuit
Reset minimization state to initial state.
Leaves
strategy,precision,tol,errordef,print_levelunchanged.
- scan(ncall: int | None = None) Minuit
Brute-force minimization.
Scans the function on a regular hypercube grid, whose bounds are defined either by parameter limits if present or by Minuit.values +/- Minuit.errors. Minuit.errors are initialized to very small values by default, too small for this scan. They should be increased before running scan or limits should be set. The scan evaluates the function exactly at the limit boundary, so the function should be defined there.
- Parameters:
ncall – Approximate number of function calls to spend on the scan. The actual number will be close to this, the scan uses ncall^(1/npar) steps per cube dimension. If no value is given, a heuristic is used to set ncall.
Notes
The scan can return an invalid minimum, this is not a cause for alarm. It just minimizes the cost function, the EDM value is only computed after the scan found a best point. If the best point still has a bad EDM value, the minimum is considered invalid. But even if it is considered valid, it is probably not accurate, since the tolerance is very lax. One should always run
migrad()after the scan.This implementation here does a full scan of the hypercube in Python. Originally, this was supposed to use MnScan from C++ Minuit2, but MnScan is unsuitable. It does a 1D scan with 41 steps (not configurable) for each parameter in sequence, so it is not actually scanning the full hypercube. It first scans one parameter, then starts the scan of the second parameter from the best value of the first and so on. This fails easily when the parameters are correlated.
- scipy(method: str | Callable = None, ncall: int | None = None, hess: Any = None, hessp: Any = None, constraints: Iterable = None, options: Dict[str, Any] | None = None) Minuit
Minimize with SciPy algorithms.
- Parameters:
method (str or Callable, optional) – Which scipy method to use.
ncall (int, optional) – Function call limit.
hess (Callable, optional) – Function that computes the Hessian matrix. It must use the exact same calling conversion as the original fcn (several arguments which are numbers or a single array argument).
hessp (Callable, optional) – Function that computes the product of the Hessian matrix with a vector. It must use the same calling conversion as the original fcn (several arguments which are numbers or a single array argument) and end with another argument which is an arbitrary vector.
constraints (scipy.optimize.LinearConstraint or) – scipy.optimize.NonlinearConstraint, optional Linear or non-linear constraints, see docs of
scipy.optimize.minimize()look for the constraints parameter. The function used in the constraint must use the exact same calling convention as the original fcn, see hess parameter for details. No parameters may be omitted in the signature, even if those parameters are not used in the constraint.options (dict, optional) – A dictionary of solver options to pass to the SciPy minimizer through the options parameter of
scipy.optimize.minimize(). See each solver method for the options it accepts.
Notes
The call limit may be violated since many algorithms checks the call limit only after a full iteraction of their algorithm, which consists of several function calls. Some algorithms do not check the number of function calls at all, in this case the call limit acts on the number of iterations of the algorithm. This issue should be fixed in scipy.
The SciPy minimizers use their own internal rule for convergence. The EDM criterion is evaluated only after the original algorithm already stopped. This means that usually SciPy minimizers will use more iterations than Migrad and the tolerance
tolhas no effect on SciPy minimizers.You can specify convergence tolerance and other options for the SciPy minimizers through the options parameter. Note that providing the SciPy options “maxiter”, “maxfev”, and/or “maxfun” (depending on the minimizer) takes precedence over providing a value for ncall. If you want to explicitly control the number of iterations or function evaluations for a particular SciPy minimizer, you should provide values for all of its relevant options.
- simplex(ncall: int | None = None) Minuit
Run Simplex minimization.
Simplex from the Minuit2 C++ library is a variant of the Nelder-Mead algorithm to find the minimum of a function. It does not make use of derivatives. The Wikipedia has a good article on the Nelder-Mead method.
- Parameters:
ncall – Approximate maximum number of calls before minimization will be aborted. If set to None, use the adaptive heuristic from the Minuit2 library (Default: None). Note: The limit may be slightly violated, because the condition is checked only after a full iteration of the algorithm, which usually performs several function calls.
Notes
The Simplex method usually converges more slowly than Migrad, but performs better in certain cases, the Rosenbrock function is a notable example. Unlike Migrad, the Simplex method does not have quadratic convergence near the minimum, so it is a good approach to run Migrad after Simplex to obtain an accurate solution in fewer steps. Simplex may also be useful to get close to the minimum from an unsuitable starting point.
The convergence criterion for Simplex is also based on EDM, but the threshold is much more lax than that of Migrad (see
Minuit.tolfor details). This was made so that Simplex stops early when getting near the minimum, to give the user a chance to switch to the more efficient Migrad algorithm to finish the minimization. Early stopping can be avoided by setting Minuit.tol to an accordingly smaller value, however.
- visualize(plot: Callable = None, **kwargs)
Visualize agreement of current model with data (requires matplotlib).
This generates a plot of the data/model agreement, using the current parameter values, if the likelihood function supports this, otherwise AttributeError is raised.
- Parameters:
plot (Callable, optional) – This function tries to call the visualize method on the cost function, which accepts the current model parameters as an array-like and potentially further keyword arguments, and draws a visualization into the current matplotlib axes. If the cost function does not provide a visualize method or if you want to override it, pass the function here.
kwargs – Other keyword arguments are forwarded to the plot function.
See also
- LEAST_SQUARES = 1.0
- LIKELIHOOD = 0.5
- property accurate: bool
Return True if the covariance matrix is accurate.
This is an alias for
iminuit.util.FMin.has_accurate_covar.See also
- property covariance: Matrix | None
Return covariance matrix.
The square-root of the diagonal elements of the covariance matrix correspond to a standard deviation for each parameter with 68 % coverage probability in the asymptotic limit (large samples). To get k standard deviations, multiply the covariance matrix with k^2.
The submatrix formed by two parameters describes an ellipse. The asymptotic coverage probabilty of the standard ellipse is lower than 68 %. It can be computed from the \(\chi^2\) distribution with 2 degrees of freedom. In general, to obtain a (hyper-)ellipsoid with coverage probability CL, one has to multiply the submatrix of the corresponding k parameters with a factor. For k = 1,2,3 and CL = 0.99
from scipy.stats import chi2 chi2(1).ppf(0.99) # 6.63... chi2(2).ppf(0.99) # 9.21... chi2(3).ppf(0.99) # 11.3...
See also
- property errordef: float
Access FCN increment above minimum that corresponds to one standard deviation.
Default value is 1.0. errordef should be 1.0 for a least-squares cost function and 0.5 for a negative log-likelihood function. See section 1.5.1 on page 6 of the
MINUIT2 User's Guide. This parameter is also called UP in MINUIT documents.If FCN has an attribute
errordef, its value is used automatically and you should not set errordef by hand. Doing so will raise a ErrordefAlreadySetWarning.For the builtin cost functions in
iminuit.cost, you don’t need to set this value, because they all have theerrordefattribute set.To make user code more readable, we provided two named constants:
m_lsq = Minuit(a_least_squares_function) m_lsq.errordef = Minuit.LEAST_SQUARES # == 1 m_nll = Minuit(a_likelihood_function) m_nll.errordef = Minuit.LIKELIHOOD # == 0.5
- property errors: ErrorView
Access parameter parabolic errors via an array-like view.
Like
values, but instead of reading or writing the values, you read or write the errors (which double as step sizes for MINUITs numerical gradient estimation). Only positive values are accepted when assigning to errors.
- property fcn: FCN
Get cost function (usually a least-squares or likelihood function).
- property fixed: FixedView
Access whether parameters are fixed via an array-like view.
Use to read or write the fixation state of a parameter based on the parameter index or the parameter name as a string. If you change the state and run
migrad(),hesse(), orminos(), the new state is used.In case of complex fits, it can help to fix some parameters first and only minimize the function with respect to the other parameters, then release the fixed parameters and minimize again starting from that state.
- property fval: float | None
Get function value at minimum.
This is an alias for
iminuit.util.FMin.fval.See also
- property g2: Callable[[ndarray], ndarray]
Get g2 function of the cost function.
- property grad: Callable[[ndarray], ndarray]
Get gradient function of the cost function.
- property hessian: Callable[[ndarray], ndarray]
Get hessian function of the cost function.
- property init_params: Params
Get list of current parameter data objects set to the initial fit state.
See also
- property limits: LimitView
Access parameter limits via a array-like view.
Use to read or write the limits of a parameter based on the parameter index or the parameter name as a string. If you change the limits and run
migrad(),hesse(), orminos(), the new state is used.In case of complex fits, it can help to limit some parameters first, run Migrad, then remove the limits and run Migrad again. Limits will bias the result only if the best fit value is outside the limits, not if it is inside. Limits will affect the estimated Hesse uncertainties if the parameter is close to a limit. They do not affect the Minos uncertainties, because those are invariant to transformations and limits are implemented via a variable transformation.
- property merrors: MErrors
Return a dict-like with Minos data objects.
The Minos data objects contain the full status information of the Minos run.
See also
- property ndof: int
Get number of degrees of freedom if cost function supports this.
To support this feature, the cost function has to report the number of data points with a property called
ndata. Unbinned cost functions should return infinity.
- property nfcn: int
Get total number of function calls.
- property nfit: int
Get number of fitted parameters (fixed parameters not counted).
- property ng2: int
Get total number of G2 calls.
- property ngrad: int
Get total number of gradient calls.
- property nhessian: int
Get total number of Hessian calls.
- property npar: int
Get number of parameters.
- property pos2var: Tuple[str, ...]
Map variable index to name.
- property precision: float | None
Access estimated precision of the cost function.
Default: None. If set to None, Minuit assumes the cost function is computed in double precision. If the precision of the cost function is lower (because it computes in single precision, for example) set this to some multiple of the smallest relative change of a parameter that still changes the function.
- property print_level: int
Access current print level.
You can assign an integer:
0: quiet (default)
1: print minimal debug messages to terminal
2: print more debug messages to terminal
3: print even more debug messages to terminal
Warning
Setting print_level has the unwanted side-effect of setting the level globally for all Minuit instances in the current Python session.
- property strategy: MnStrategy
Access current minimization strategy.
You can assign an integer:
0: Fast. Does not check a user-provided gradient. Does not improve Hesse matrix at minimum. Extra call to
hesse()aftermigrad()is always needed for good error estimates. If you pass a user-provided gradient to MINUIT, convergence is faster.1: Default. Checks user-provided gradient against numerical gradient. Checks and usually improves Hesse matrix at minimum. Extra call to
hesse()aftermigrad()is usually superfluous. If you pass a user-provided gradient to MINUIT, convergence is slower.2: Careful. Like 1, but does extra checks of intermediate Hessian matrix during minimization. The effect in benchmarks is a somewhat improved accuracy at the cost of more function evaluations. A similar effect can be achieved by reducing the tolerance
tolfor convergence at any strategy level.
- property throw_nan: bool
Access whether to raise runtime error if the function evaluates to NaN.
If you set this to True, an error is raised whenever the function evaluates to NaN.
- property tol: float
Access tolerance for convergence with the EDM criterion.
Minuit detects converge with the EDM criterion. EDM stands for Estimated Distance to Minimum, it is mathematically described in the MINUIT paper. The EDM criterion is well suited for statistical cost functions, since it stops the minimization when parameter improvements become small compared to parameter uncertainties.
The convergence is detected when edm < edm_max, where edm_max is calculated as
Migrad: edm_max = 0.002 * tol * errordef
Simplex: edm_max = tol * errordef
Users can set tol (default: 0.1) to a different value to either speed up convergence at the cost of a larger error on the fitted parameters and possibly invalid estimates for parameter uncertainties or smaller values to get more accurate parameter values, although this should never be necessary as the default is fine.
If the tolerance is set to a very small value or zero, Minuit will use an internal lower limit for the tolerance. To restore the default use, one can assign None.
Under some circumstances, Migrad is allowed to violate edm_max by a factor of 10. Users should not try to detect convergence by comparing edm with edm_max, but query
iminuit.util.FMin.is_above_max_edm.
- property valid: bool
Return True if the function minimum is valid.
This is an alias for
iminuit.util.FMin.is_valid.See also
- property values: ValueView
Access parameter values via an array-like view.
Use to read or write current parameter values based on the parameter index or the parameter name as a string. If you change a parameter value and run
migrad(), the minimization will start from that value, similar forhesse()andminos().
- property var2pos: Dict[str, int]
Map variable name to index.
Scipy-like interface
- iminuit.minimize(fun, x0, args=(), method='migrad', jac=None, hess=None, hessp=None, bounds=None, constraints=None, tol=None, callback=None, options=None)
Interface to MIGRAD using the
scipy.optimize.minimizeAPI.This function provides the same interface as
scipy.optimize.minimize. If you are familiar with the latter, this allows you to use Minuit with a quick start. Eventually, you still may want to learn the interface of theMinuitclass, as it provides more functionality if you are interested in parameter uncertainties.For a general description of the arguments of this function, see
scipy.optimize.minimize. We list only a few in the following.- Parameters:
method (str) – Allowed values are “migrad” or “simplex”. Default: “migrad”.
options (dict) – Can be used to pass special settings to Minuit. All are optional. The following options are supported. disp (bool): Set to true to print convergence messages. Default: False. stra (int): Minuit strategy (0: fast/inaccurate, 1: balanced, 2: slow/accurate). Default: 1. maxfun (int): Maximum allowed number of iterations. Default: None. maxfev (int): Deprecated alias for maxfun. eps (sequence): Initial step size to numerical compute derivative. Minuit automatically refines this in subsequent iterations and is very insensitive to the initial choice. Default: 1.
- Returns:
Dict with attribute access that holds the result. It contains the following lists of fields. x (ndarray): Solution of optimization. fun (float): Value of objective function at minimum. message (str): Description of cause of termination. hess_inv (ndarray): Inverse of Hesse matrix at minimum (may not be exact). nfev (int): Number of function evaluations. njev (int): Number of jacobian evaluations. minuit (Minuit): Minuit object internally used to do the minimization. Use this to extract more information about the parameter errors.
- Return type:
OptimizeResult
Cost functions
Standard cost functions to minimize for statistical fits.
We provide these for convenience, so that you do not have to write your own for standard fits. The cost functions optionally use Numba to accelerate some calculations, if Numba is installed.
There is no need to set iminuit.Minuit.errordef manually for any of these
cost functions. iminuit.Minuit automatically uses the correct value, which is
provided by each cost function with the attribute Cost.errordef.
What to use when
Fit a normalised probability density to data
Data are not binned:
UnbinnedNLLData are binned:
BinnedNLL, also supports histogram of weighted samples
Fit a density to data, density is not normalised
Data are not binned:
ExtendedUnbinnedNLLData are binned:
ExtendedBinnedNLL, also supports histogram of weighted samples
Fit a template to binned data with bin-wise uncertainties on the template
Template, also supports weighted data and weighted template histograms
Fit of a function f(x) to (x, y, yerror) pairs with normal-distributed fluctuations. x is one- or multi-dimensional, y is one-dimensional.
y values contain no outliers:
LeastSquaresy values contain outliers:
LeastSquareswith loss function set to “soft_l1”
Include constraints from external fits or apply regularisation
Combining cost functions
All cost functions can be added, which generates a new combined cost function. Parameters with the same name are shared between component cost functions. Use this to constrain one or several parameters with different data sets and using different statistical models for each data set. Gaussian penalty terms can also be added to the cost function to introduce external knowledge about a parameter.
Model parameter limits
The Minuit algorithms support box constrains in parameter space. A user-defined model
can declare that a parameter is only valid over an interval on the real line with the
Annotated type annotation, see iminuit.Minuit for details. A typical
example is the sigma parameter of a normal distribution, which must be positive. The
cost functions defined here propagate this information to iminuit.Minuit.
Note: The Template declares that the template amplitudes must be non-negative,
which is usually the right choice, however, it may be desirable to fit templates which
can have negative amplitudes. To achieve this, simply reset the limits with
iminuit.Minuit.limits after creating the Minuit instance.
User-defined gradients
If the user provides a model gradient, the cost functions defined here except
Template will then also make their gradient available, which is then
automatically used by iminuit.Minuit (see the constructor for details) to
potentially improve the fit (improve convergence or robustness).
Note that it is perfectly normal to use Minuit without a user-defined gradient, and Minuit does not always benefit from a user-defined gradient. If the gradient is expensive to compute, the time to converge may increase. If you have trouble with the fitting process, it is unlikely that the issues are resolved by a user-defined gradient.
Notes
The cost functions defined here have been optimized with knowledge about implementation details of Minuit to give the highest accucary and the most robust results, so they should perform well. If you have trouble with your own implementations, try these.
The binned versions of the log-likelihood fits support weighted samples. For each bin of the histogram, the sum of weights and the sum of squared weights is needed then, see class documentation for details.
- class iminuit.cost.BinnedNLL(n: ArrayLike, xe: ArrayLike | Sequence[ArrayLike], cdf: Model, *, verbose: int = 0, grad: ModelGradient | None = None, use_pdf: str = '', name: Sequence[str] | None = None)
Binned negative log-likelihood.
Use this if only the shape of the fitted PDF is of interest and the data is binned. This cost function works with normal and weighted histograms. The histogram can be one- or multi-dimensional.
The cost function has a minimum value that is asymptotically chi2-distributed. It is constructed from the log-likelihood assuming a multivariate-normal distribution and using the saturated model as a reference, see
multinomial_chi2()for details.When this class is used with weighted data, we use the Bohm-Zech transform for Poisson-distributed data and the
poisson_chi2()cost function, becausemultinomial_chi2()yields biased results for weighted data. The reasoning for this choice is thatmultinomial_chi2()andpoisson_chi2()yield the same result for a model which predicts probabilities and expected counts are computed by multiplying the probability with the total number of counts. Thus we can derivemultinomial_chi2()as a special case ofpoisson_chi2()in case of unweighted data, but this mathematical equivalence is gone when data are weighted. The correct cost function is thenpoisson_chi2().Initialize cost function with data and model.
- Parameters:
n (array-like) – Histogram counts. If this is an array with dimension D+1, where D is the number of histogram axes, then the last dimension must have two elements and is interpreted as pairs of sum of weights and sum of weights squared.
xe (array-like or collection of array-like) – Bin edge locations, must be len(n) + 1, where n is the number of bins. If the histogram has more than one axis, xe must be a collection of the bin edge locations along each axis.
cdf (callable) – Cumulative density function of the form f(xe, par0, par1, …, parN), where xe is a bin edge and par0, … are model parameters. The corresponding density must be normalized to unity over the space covered by the histogram. If the model is multivariate, xe must be an array-like with shape (D, N), where D is the dimension and N is the number of points where the model is evaluated.
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
grad (callable or None, optional) – Optionally pass the gradient of the cdf (Default is None). Has the same calling signature like the cdf, but must return an array with the shape (K, N), where N is the number of data points and K is the number of parameters. The gradient can be used by Minuit to improve or speed up convergence.
use_pdf (str, optional) – Either “”, “numerical”, or “approximate” (Default is “”). If the model cdf is not available, but the model pdf is, this option can be set to “numerical” or “approximate” to compute the integral of the pdf over the bin patch. The option “numerical” uses numerical integration, which is accurate but computationally expensive and only supported for 1D histograms. The option “approximate” uses the zero-order approximation of evaluating the pdf at the bin center, multiplied with the bin area. This is fast and works in higher dimensions, but can lead to biased results if the curvature of the pdf inside the bin is significant.
name (sequence of str or None, optional) – Optional names for each parameter of the model (in order). Must have the same length as there are model parameters. Default is None.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- prediction(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]] | Tuple[ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]]]
Return the bin-wise expectation for the fitted model.
- Parameters:
args (array-like) – Parameter values.
- Returns:
Model prediction for each bin. The expectation is always returned for all bins, even if some bins are temporarily masked.
- Return type:
NDArray
- pulls(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Return studentized residuals (aka pulls).
- Parameters:
args (sequence of float) – Parameter values.
- Returns:
Array of pull values. If the cost function is masked, the array contains NaN values where the mask value is False.
- Return type:
array
Notes
Pulls allow one to estimate how well a model fits the data. A pull is a value computed for each data point. It is given by (observed - predicted) / standard-deviation. If the model is correct, the expectation value of each pull is zero and its variance is one in the asymptotic limit of infinite samples. Under these conditions, the chi-square statistic is computed from the sum of pulls squared has a known probability distribution if the model is correct. It therefore serves as a goodness-of-fit statistic.
Beware: the sum of pulls squared in general is not identical to the value returned by the cost function, even if the cost function returns a chi-square distributed test-statistic. The cost function is computed in a slightly differently way that makes the return value approach the asymptotic chi-square distribution faster than a test statistic based on sum of pulls squared. In summary, only use pulls for plots. Compute the chi-square test statistic directly from the cost function.
- visualize(args: Sequence[float]) None
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current axes.
- Parameters:
args (sequence of float) – Parameter values.
Notes
The automatically provided visualization for multi-dimensional data set is often not very pretty, but still helps to judge whether the fit is reasonable. Since there is no obvious way to draw higher dimensional data with error bars in comparison to a model, the visualization shows all data bins as a single sequence.
- property cdf
Get cumulative density function.
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property n
Return data samples.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- property xe
Access bin edges.
- class iminuit.cost.Constant(value: float)
Cost function that represents a constant.
If your cost function produces results that are far away from O(1), adding a constant that brings the value closer to zero may improve the numerical stability.
Initialize constant with a value.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- property has_grad: bool
Return True if cost function can compute a gradient.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- class iminuit.cost.CostSum(*items: Cost | float)
Sum of cost functions.
Users do not need to create objects of this class themselves. They should just add cost functions, for example:
nll = UnbinnedNLL(...) lsq = LeastSquares(...) ncs = NormalConstraint(...) csum = nll + lsq + ncs
CostSum is used to combine data from different experiments or to combine normal cost functions with penalty terms (see NormalConstraint).
The parameters of CostSum are the union of all parameters of its constituents.
Supports the sequence protocol to access the constituents.
Warning
CostSum does not support cost functions that accept a parameter array, because the function signature does not allow one to determine how many parameters are accepted by the function and which parameters overlap between different cost functions.
Initialize with cost functions.
- Parameters:
*items (Cost) – Cost functions. May also be other CostSum functions.
- count(value) integer -- return number of occurrences of value
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- index(value[, start[, stop]]) integer -- return first index of value.
Raises ValueError if the value is not present.
Supporting start and stop arguments is optional, but recommended.
- visualize(args: Sequence[float], component_kwargs: Dict[int, Dict[str, Any]] = None)
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current figure. Subplots are created to visualize each part of the cost function, the figure height is increased accordingly. Parts without a visualize method are silently ignored.
- Parameters:
args (array-like) – Parameter values.
component_kwargs (dict of dicts, optional) – Dict that maps an index to dict of keyword arguments. This can be used to pass keyword arguments to a visualize method of a component with that index.
**kwargs – Other keyword arguments are forwarded to all components.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- class iminuit.cost.ExtendedBinnedNLL(n: ArrayLike, xe: ArrayLike | Sequence[ArrayLike], scaled_cdf: Model, *, verbose: int = 0, grad: ModelGradient | None = None, use_pdf: str = '', name: Sequence[str] | None = None)
Binned extended negative log-likelihood.
Use this if shape and normalization of the fitted PDF are of interest and the data is binned. This cost function works with normal and weighted histograms. The histogram can be one- or multi-dimensional.
The cost function works for both weighted data. The cost function assumes that the weights are independent of the data. This is not the case for sWeights, and the uncertaintes for results obtained with sWeights will only be approximately correct, see C. Langenbruch, Eur.Phys.J.C 82 (2022) 5, 393.
The cost function has a minimum value that is asymptotically chi2-distributed. It is constructed from the log-likelihood assuming a poisson distribution and using the saturated model as a reference.
Initialize cost function with data and model.
- Parameters:
n (array-like) – Histogram counts. If this is an array with dimension D+1, where D is the number of histogram axes, then the last dimension must have two elements and is interpreted as pairs of sum of weights and sum of weights squared.
xe (array-like or collection of array-like) – Bin edge locations, must be len(n) + 1, where n is the number of bins. If the histogram has more than one axis, xe must be a collection of the bin edge locations along each axis.
scaled_cdf (callable) – Scaled Cumulative density function of the form f(xe, par0, [par1, …]), where xe is a bin edge and par0, … are model parameters. If the model is multivariate, xe must be an array-like with shape (D, N), where D is the dimension and N is the number of points where the model is evaluated.
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
grad (callable or None, optional) – Optionally pass the gradient of the cdf (Default is None). Has the same calling signature like the cdf, but must return an array with the shape (K, N), where N is the number of data points and K is the number of parameters. The gradient can be used by Minuit to improve or speed up convergence.
use_pdf (str, optional) – Either “”, “numerical”, or “approximate”. If the model cdf is not available, but the model pdf is, this option can be set to “numerical” or “approximate” to compute the integral of the pdf over the bin patch. The option “numerical” uses numerical integration, which is accurate but computationally expensive and only supported for 1D histograms. The option “approximate” uses the zero-order approximation of evaluating the pdf at the bin center, multiplied with the bin area. This is fast and works in higher dimensions, but can lead to biased results if the curvature of the pdf inside the bin is significant.
name (sequence of str or None, optional) – Optional names for each parameter of the model (in order). Must have the same length as there are model parameters. Default is None.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- prediction(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]] | Tuple[ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]]]
Return the bin-wise expectation for the fitted model.
- Parameters:
args (array-like) – Parameter values.
- Returns:
Model prediction for each bin. The expectation is always returned for all bins, even if some bins are temporarily masked.
- Return type:
NDArray
- pulls(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Return studentized residuals (aka pulls).
- Parameters:
args (sequence of float) – Parameter values.
- Returns:
Array of pull values. If the cost function is masked, the array contains NaN values where the mask value is False.
- Return type:
array
Notes
Pulls allow one to estimate how well a model fits the data. A pull is a value computed for each data point. It is given by (observed - predicted) / standard-deviation. If the model is correct, the expectation value of each pull is zero and its variance is one in the asymptotic limit of infinite samples. Under these conditions, the chi-square statistic is computed from the sum of pulls squared has a known probability distribution if the model is correct. It therefore serves as a goodness-of-fit statistic.
Beware: the sum of pulls squared in general is not identical to the value returned by the cost function, even if the cost function returns a chi-square distributed test-statistic. The cost function is computed in a slightly differently way that makes the return value approach the asymptotic chi-square distribution faster than a test statistic based on sum of pulls squared. In summary, only use pulls for plots. Compute the chi-square test statistic directly from the cost function.
- visualize(args: Sequence[float]) None
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current axes.
- Parameters:
args (sequence of float) – Parameter values.
Notes
The automatically provided visualization for multi-dimensional data set is often not very pretty, but still helps to judge whether the fit is reasonable. Since there is no obvious way to draw higher dimensional data with error bars in comparison to a model, the visualization shows all data bins as a single sequence.
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property n
Return data samples.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property scaled_cdf
Get integrated density model.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- property xe
Access bin edges.
- class iminuit.cost.ExtendedUnbinnedNLL(data: ArrayLike, scaled_pdf: Model, *, verbose: int = 0, log: bool = False, grad: ModelGradient | None = None, name: Sequence[str] | None = None)
Unbinned extended negative log-likelihood.
Use this if shape and normalization of the fitted PDF are of interest and the original unbinned data is available. The data can be one- or multi-dimensional.
Initialize cost function with data and model.
- Parameters:
data (array-like) – Sample of observations. If the observations are multidimensional, data must have the shape (D, N), where D is the number of dimensions and N the number of data points.
scaled_pdf (callable) – Density function of the form f(data, par0, [par1, …]), where data is the sample and par0, … are model parameters. Must return a tuple (<integral over f in data window>, <f evaluated at data points>). The first value is the density integrated over the data window, the interval that we consider for the fit. For example, if the data are exponentially distributed, but we fit only the interval (0, 5), then the first value is the density integrated from 0 to 5. If the data are multivariate, data passed to f has shape (D, N), where D is the number of dimensions and N the number of data points.
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
log (bool, optional) – Distributions of the exponential family (normal, exponential, poisson, …) allow one to compute the logarithm of the pdf directly, which is more accurate and efficient than effectively doing
log(exp(logpdf)). Set this to True, if the model returns the logarithm of the density as the second argument instead of the density. Default is False.grad (callable or None, optional) – Optionally pass the gradient of the density function. Has the same calling signature like the density function, but must return two arrays. The first array has shape (K,) where K are the number of parameters, while the second has shape (K, N), where N is the number of data points. The first array is the gradient of the integrated density. The second array is the gradient of the density itself. If log is True, the second array must be the gradient of the log-density instead. The gradient can be used by Minuit to improve or speed up convergence and to compute the sandwich estimator for the variance of the parameter estimates. Default is None.
name (sequence of str or None, optional) – Optional names for each parameter of the model (in order). Must have the same length as there are model parameters. Default is None.
- covariance(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Estimate covariance of the parameters with the sandwich estimator.
This requires that the model gradient is provided, and that the arguments are the maximum-likelihood estimates. The sandwich estimator is only asymptotically correct.
- Parameters:
*args (float) – Maximum-likelihood estimates of the parameter values.
- Returns:
The array has shape (K, K) for K arguments.
- Return type:
ndarray of float
- fisher_information(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Estimate Fisher information for model and sample.
The estimated Fisher information is only meaningful if the arguments provided are estimates of the true values.
- Parameters:
*args (float) – Estimates of model parameters.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property pdf
Get probability density model.
- property scaled_pdf
Get density model.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- class iminuit.cost.LeastSquares(x: ArrayLike, y: ArrayLike, yerror: ArrayLike, model: Model, *, loss: str | LossFunction = 'linear', verbose: int = 0, grad: ModelGradient | None = None, name: Sequence[str] | None = None)
Least-squares cost function (aka chisquare function).
Use this if you have data of the form (x, y +/- yerror), where x can be one-dimensional or multi-dimensional, but y is always one-dimensional. See
__init__()for details on how to use a multivariate model.Initialize cost function with data and model.
- Parameters:
x (array-like) – Locations where the model is evaluated. If the model is multivariate, x must have shape (D, N), where D is the number of dimensions and N the number of data points.
y (array-like) – Observed values. Must have the same length as x.
yerror (array-like or float) – Estimated uncertainty of observed values. Must have same shape as y or be a scalar, which is then broadcasted to same shape as y.
model (callable) – Function of the form f(x, par0, [par1, …]) whose output is compared to observed values, where x is the location and par0, … are model parameters. If the model is multivariate, x has shape (D, N), where D is the number of dimensions and N the number of data points.
loss (str or callable, optional) – The loss function can be modified to make the fit robust against outliers, see scipy.optimize.least_squares for details. Only “linear” (default) and “soft_l1” are currently implemented, but users can pass any loss function as this argument. It should be a monotonic, twice differentiable function, which accepts the squared residual and returns a modified squared residual.
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
Notes
Alternative loss functions make the fit more robust against outliers by weakening the pull of outliers. The mechanical analog of a least-squares fit is a system with attractive forces. The points pull the model towards them with a force whose potential is given by \(rho(z)\) for a squared-offset \(z\). The plot shows the standard potential in comparison with the weaker soft-l1 potential, in which outliers act with a constant force independent of their distance.
(
Source code,png,hires.png,pdf)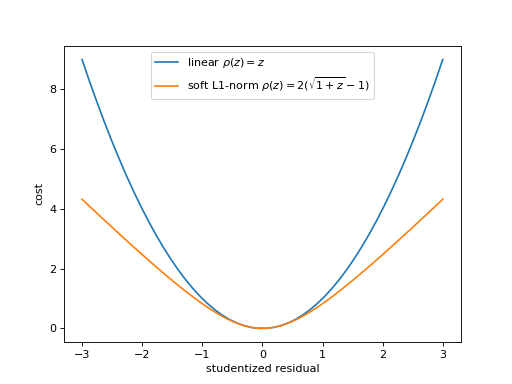
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- prediction(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Return the prediction from the fitted model.
- Parameters:
args (array-like) – Parameter values.
- Returns:
Model prediction for each bin.
- Return type:
NDArray
- pulls(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Return studentized residuals (aka pulls).
- Parameters:
args (sequence of float) – Parameter values.
- Returns:
Array of pull values. If the cost function is masked, the array contains NaN values where the mask value is False.
- Return type:
array
Notes
Pulls allow one to estimate how well a model fits the data. A pull is a value computed for each data point. It is given by (observed - predicted) / standard-deviation. If the model is correct, the expectation value of each pull is zero and its variance is one in the asymptotic limit of infinite samples. Under these conditions, the chi-square statistic is computed from the sum of pulls squared has a known probability distribution if the model is correct. It therefore serves as a goodness-of-fit statistic.
Beware: the sum of pulls squared in general is not identical to the value returned by the cost function, even if the cost function returns a chi-square distributed test-statistic. The cost function is computed in a slightly differently way that makes the return value approach the asymptotic chi-square distribution faster than a test statistic based on sum of pulls squared. In summary, only use pulls for plots. Compute the chi-square test statistic directly from the cost function.
- visualize(args: ArrayLike, model_points: int | Sequence[float] = 0) Tuple[Tuple[ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]]], Tuple[ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]]]]
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current axes.
- Parameters:
args (array-like) – Parameter values.
model_points (int or array-like, optional) – How many points to use to draw the model. Default is 0, in this case an smart sampling algorithm selects the number of points. If array-like, it is interpreted as the point locations.
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property loss
Get loss function.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property model
Get model of the form y = f(x, par0, [par1, …]).
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- property x
Get explanatory variables.
- property y
Get samples.
- property yerror
Get sample uncertainties.
- class iminuit.cost.NormalConstraint(args: str | Iterable[str], value: ArrayLike, error: ArrayLike)
Gaussian penalty for one or several parameters.
The Gaussian penalty acts like a pseudo-measurement of the parameter itself, based on a (multi-variate) normal distribution. Penalties can be set for one or several parameters at once (which is more efficient). When several parameter are constrained, one can specify the full covariance matrix of the parameters.
Notes
It is sometimes necessary to add a weak penalty on a parameter to avoid instabilities in the fit. A typical example in high-energy physics is the fit of a signal peak above some background. If the amplitude of the peak vanishes, the shape parameters of the peak become unconstrained and the fit becomes unstable. This can be avoided by adding weak (large uncertainty) penalty on the shape parameters whose pull is negligible if the peak amplitude is non-zero.
This class can also be used to approximately include external measurements of some parameters, if the original cost function is not available or too costly to compute. If the external measurement was performed in the asymptotic limit with a large sample, a Gaussian penalty is an accurate statistical representation of the external result.
Initialize the normal constraint with expected value(s) and error(s).
- Parameters:
args (str or sequence of str) – Parameter name(s).
value (float or array-like) – Expected value(s). Must have same length as args.
error (float or array-like) – Expected error(s). If 1D, must have same length as args. If 2D, must be the covariance matrix of the parameters.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- visualize(args: ArrayLike)
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current axes.
- Parameters:
args (array-like) – Parameter values.
- property covariance
Get expected covariance of parameters.
Can be 1D (diagonal of covariance matrix) or 2D (full covariance matrix).
- property has_grad: bool
Return True if cost function can compute a gradient.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property value
Get expected parameter values.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- class iminuit.cost.Template(n: ArrayLike, xe: ArrayLike | Sequence[ArrayLike], model_or_template: Collection[Model | ArrayLike], *, name: Sequence[str] | None = None, verbose: int = 0, method: str = 'da')
Binned cost function for a template fit with uncertainties on the template.
This cost function is for a mixture of components. Use this if the sample originate from two or more components and you are interested in estimating the yield that originates from one or more components. In high-energy physics, one component is often a peaking signal over a smooth background component. A component can be described by a parametric model or a template.
A parametric model is accepted in form of a scaled cumulative density function, while a template is a non-parametric shape estimate obtained by histogramming a Monte-Carlo simulation. Even if the Monte-Carlo simulation is asymptotically correct, estimating the shape from a finite simulation sample introduces some uncertainty. This cost function takes that additional uncertainty into account.
There are several ways to fit templates and take the sampling uncertainty into account. Barlow and Beeston [1] found an exact likelihood for this problem, with one nuisance parameter per component per bin. Solving this likelihood is somewhat challenging though. The Barlow-Beeston likelihood also does not handle the additional uncertainty in weighted templates unless the weights per bin are all equal.
Other works [2] [3] [4] describe likelihoods that use only one nuisance parameter per bin, which is an approximation. Some marginalize over the nuisance parameters with some prior, while others profile over the nuisance parameter. This class implements several of these methods. The default method is the one which performs best under most conditions, according to current knowledge. The default may change if this assessment changes.
The cost function returns an asymptotically chi-square distributed test statistic, except for the method “asy”, where it is the negative logarithm of the marginalised likelihood instead. The standard transform [5] which we use convert likelihoods into test statistics only works for (profiled) likelihoods, not for likelihoods marginalized over a prior.
All methods implemented here have been generalized to work with both weighted data and weighted templates, under the assumption that the weights are independent of the data. This is not the case for sWeights, and the uncertaintes for results obtained with sWeights will only be approximately correct [6]. The methods have been further generalized to allow fitting a mixture of parametric models and templates.
Initialize cost function with data and model.
- Parameters:
n (array-like) – Histogram counts. If this is an array with dimension D+1, where D is the number of histogram axes, then the last dimension must have two elements and is interpreted as pairs of sum of weights and sum of weights squared.
xe (array-like or collection of array-like) – Bin edge locations, must be len(n) + 1, where n is the number of bins. If the histogram has more than one axis, xe must be a collection of the bin edge locations along each axis.
model_or_template (collection of array-like or callable) – Collection of models or arrays. An array represent the histogram counts of a template. The template histograms must use the same axes as the data histogram. If the counts are represented by an array with dimension D+1, where D is the number of histogram axes, then the last dimension must have two elements and is interpreted as pairs of sum of weights and sum of weights squared. Callables must return the model cdf evaluated as xe.
name (sequence of str or None, optional) – Optional name for the yield of each template and the parameter of each model (in order). Must have the same length as there are templates and model parameters in templates_or_model. Default is None.
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
method ({"jsc", "asy", "da"}, optional) – Which method to use. “jsc”: Conway’s method [2]. “asy”: ASY method [3]. “da”: DA method [4]. Default is “da”, which to current knowledge offers the best overall performance. The default may change in the future, so please set this parameter explicitly in code that has to be stable. For all methods except the “asy” method, the minimum value is chi-square distributed.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- prediction(args: Sequence[float]) Tuple[ndarray[tuple[Any, ...], dtype[_ScalarT]], ndarray[tuple[Any, ...], dtype[_ScalarT]]]
Return the fitted template and its standard deviation.
This returns the prediction from the templates, the sum over the products of the template yields with the normalized templates. The standard deviation is returned as the second argument, this is the estimated uncertainty of the fitted template alone. It is obtained via error propagation, taking the statistical uncertainty in the template into account, but regarding the yields as parameters without uncertainty.
- Parameters:
args (array-like) – Parameter values.
- Returns:
y, yerr – Template prediction and its standard deviation, based on the statistical uncertainty of the template only.
- Return type:
NDArray, NDArray
- pulls(args: Sequence[float]) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Return studentized residuals (aka pulls).
- Parameters:
args (sequence of float) – Parameter values.
- Returns:
Array of pull values. If the cost function is masked, the array contains NaN values where the mask value is False.
- Return type:
array
Notes
Pulls allow one to estimate how well a model fits the data. A pull is a value computed for each data point. It is given by (observed - predicted) / standard-deviation. If the model is correct, the expectation value of each pull is zero and its variance is one in the asymptotic limit of infinite samples. Under these conditions, the chi-square statistic is computed from the sum of pulls squared has a known probability distribution if the model is correct. It therefore serves as a goodness-of-fit statistic.
Beware: the sum of pulls squared in general is not identical to the value returned by the cost function, even if the cost function returns a chi-square distributed test-statistic. The cost function is computed in a slightly differently way that makes the return value approach the asymptotic chi-square distribution faster than a test statistic based on sum of pulls squared. In summary, only use pulls for plots. Compute the chi-square test statistic directly from the cost function.
- visualize(args: Sequence[float]) None
Visualize data and model agreement (requires matplotlib).
The visualization is drawn with matplotlib.pyplot into the current axes.
- Parameters:
args (sequence of float) – Parameter values.
Notes
The automatically provided visualization for multi-dimensional data set is often not very pretty, but still helps to judge whether the fit is reasonable. Since there is no obvious way to draw higher dimensional data with error bars in comparison to a model, the visualization shows all data bins as a single sequence.
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property n
Return data samples.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- property xe
Access bin edges.
- class iminuit.cost.UnbinnedNLL(data: ArrayLike, pdf: Model, *, verbose: int = 0, log: bool = False, grad: ModelGradient | None = None, name: Sequence[str] | None = None)
Unbinned negative log-likelihood.
Use this if only the shape of the fitted PDF is of interest and the original unbinned data is available. The data can be one- or multi-dimensional.
Initialize UnbinnedNLL with data and model.
- Parameters:
data (array-like) – Sample of observations. If the observations are multidimensional, data must have the shape (D, N), where D is the number of dimensions and N the number of data points.
pdf (callable) – Probability density function of the form f(data, par0, [par1, …]), where data is the data sample and par0, … are model parameters. If the data are multivariate, data passed to f has shape (D, N), where D is the number of dimensions and N the number of data points. Must return an array with the shape (N,).
verbose (int, optional) – Verbosity level. 0: is no output (default). 1: print current args and negative log-likelihood value.
log (bool, optional) – Distributions of the exponential family (normal, exponential, poisson, …) allow one to compute the logarithm of the pdf directly, which is more accurate and efficient than numerically computing
log(pdf). Set this to True, if the model returns the logpdf instead of the pdf. Default is False.grad (callable or None, optional) – Optionally pass the gradient of the pdf. Has the same calling signature like the pdf, but must return an array with the shape (K, N), where N is the number of data points and K is the number of parameters. If log is True, the function must return the gradient of the logpdf instead of the pdf. The gradient can be used by Minuit to improve or speed up convergence and to compute the sandwich estimator for the variance of the parameter estimates. Default is None.
name (sequence of str or None, optional) – Optional names for each parameter of the model (in order). Must have the same length as there are model parameters. Default is None.
- covariance(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Estimate covariance of the parameters with the sandwich estimator.
This requires that the model gradient is provided, and that the arguments are the maximum-likelihood estimates. The sandwich estimator is only asymptotically correct.
- Parameters:
*args (float) – Maximum-likelihood estimates of the parameter values.
- Returns:
The array has shape (K, K) for K arguments.
- Return type:
ndarray of float
- fisher_information(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Estimate Fisher information for model and sample.
The estimated Fisher information is only meaningful if the arguments provided are estimates of the true values.
- Parameters:
*args (float) – Estimates of model parameters.
- grad(*args: float) ndarray[tuple[Any, ...], dtype[_ScalarT]]
Compute gradient of the cost function.
This requires that a model gradient is provided.
- Parameters:
*args (float) – Parameter values.
- Returns:
The length of the array is equal to the length of args.
- Return type:
ndarray of float
- property data
Return data samples.
- property has_grad: bool
Return True if cost function can compute a gradient.
- property mask
Boolean array, array of indices, or None.
If not None, only values selected by the mask are considered. The mask acts on the first dimension of a value array, i.e. values[mask]. Default is None.
- property ndata
Return number of points in least-squares fits or bins in a binned fit.
Infinity is returned if the cost function is unbinned. This is used by Minuit to compute the reduced chi2, a goodness-of-fit estimate.
- property npar
Return total number of model parameters.
- property pdf
Get probability density model.
- property scaled_pdf
Get number density model.
- property verbose
Access verbosity level.
Set this to 1 to print all function calls with input and output.
- iminuit.cost.chi2(y: ArrayLike, ye: ArrayLike, ym: ArrayLike) float
Compute (potentially) chi2-distributed cost.
The value returned by this function is chi2-distributed, if the observed values are normally distributed around the expected values with the provided standard deviations.
- Parameters:
y (array-like with shape (N,)) – Observed values.
ye (array-like with shape (N,)) – Uncertainties of values.
ym (array-like with shape (N,)) – Expected values.
- Returns:
Value of cost function.
- Return type:
float
- iminuit.cost.multinomial_chi2(n: ArrayLike, mu: ArrayLike) float
Compute asymptotically chi2-distributed cost for multinomially-distributed data.
See Baker & Cousins, NIM 221 (1984) 437-442.
- Parameters:
n (array-like) – Observed counts.
mu (array-like) – Expected counts. Must satisfy sum(mu) == sum(n).
- Returns:
Cost function value.
- Return type:
float
Notes
The implementation makes the result asymptotically chi2-distributed, which helps to maximise the numerical accuracy for Minuit.
- iminuit.cost.poisson_chi2(n: ArrayLike, mu: ArrayLike) float
Compute asymptotically chi2-distributed cost for Poisson-distributed data.
See Baker & Cousins, NIM 221 (1984) 437-442.
- Parameters:
n (array-like) – Observed counts.
mu (array-like) – Expected counts per bin.
- Returns:
Cost function value.
- Return type:
float
Notes
The implementation makes the result asymptotically chi2-distributed, which helps to maximise the numerical accuracy for Minuit.
If sum(mu) == sum(n), the result is equal to
multinomial_chi2().
- iminuit.cost.template_chi2_da(n: ArrayLike, mu: ArrayLike, mu_var: ArrayLike) float
Compute asymptotically chi2-distributed cost for a template fit.
H.P. Dembinski, A. Abdelmotteleb, https://doi.org/10.48550/arXiv.2206.12346
- Parameters:
n (array-like) – Observed counts.
mu (array-like) – Expected counts. This is the sum of the normalised templates scaled with the component yields.
mu_var (array-like) – Expected variance of mu. Must be positive everywhere.
- Returns:
Asymptotically chi-square-distributed test statistic.
- Return type:
float
- iminuit.cost.template_chi2_jsc(n: ArrayLike, mu: ArrayLike, mu_var: ArrayLike) float
Compute asymptotically chi2-distributed cost for a template fit.
J.S. Conway, PHYSTAT 2011, https://doi.org/10.48550/arXiv.1103.0354
- Parameters:
n (array-like) – Observed counts.
mu (array-like) – Expected counts. This is the sum of the normalised templates scaled with the component yields. Must be positive everywhere.
mu_var (array-like) – Expected variance of mu. Must be positive everywhere.
- Returns:
Asymptotically chi-square-distributed test statistic.
- Return type:
float
Notes
The implementation deviates slightly from the paper by making the result asymptotically chi2-distributed, which helps to maximise the numerical accuracy for Minuit.
- iminuit.cost.template_nll_asy(n: ArrayLike, mu: ArrayLike, mu_var: ArrayLike) float
Compute marginalized negative log-likelikihood for a template fit.
This is the negative logarithm of equation 3.15 of the paper by C.A. Argüelles, A. Schneider, T. Yuan, https://doi.org/10.1007/JHEP06(2019)030.
The authors use a Bayesian approach and integrate over the nuisance parameters. Like the other Barlow-Beeston-lite methods, this is an approximation. The resulting likelihood cannot be turned into an asymptotically chi-square distributed test statistic as detailed in Baker & Cousins, NIM 221 (1984) 437-442.
- Parameters:
n (array-like) – Observed counts.
mu (array-like) – Expected counts. This is the sum of the normalised templates scaled with the component yields.
mu_var (array-like) – Expected variance of mu. Must be positive everywhere.
- Returns:
Negative log-likelihood function value.
- Return type:
float
Utilities
Data classes and utilities used by iminuit.Minuit.
You can look up the interface of data classes that iminuit uses here.
- exception iminuit.util.HesseFailedWarning
HESSE failed warning.
- add_note()
Exception.add_note(note) – add a note to the exception
- with_traceback()
Exception.with_traceback(tb) – set self.__traceback__ to tb and return self.
- exception iminuit.util.IMinuitWarning
Generic iminuit warning.
- add_note()
Exception.add_note(note) – add a note to the exception
- with_traceback()
Exception.with_traceback(tb) – set self.__traceback__ to tb and return self.
- exception iminuit.util.PerformanceWarning
Warning about performance issues.
- add_note()
Exception.add_note(note) – add a note to the exception
- with_traceback()
Exception.with_traceback(tb) – set self.__traceback__ to tb and return self.
- class iminuit.util.FMin(fmin: Any, algorithm: str, nfcn: int, ngrad: int, ng2: int, nhessian: int, ndof: int, edm_goal: float, time: float)
Function minimum view.
This object provides detailed metadata about the function minimum. Inspect this to check what exactly happened if the fit did not converge. Use the attribute
iminuit.Minuit.fminto get the best fit values, their uncertainties, or the function value at the minimum. For convenience, you can also get a basic OK fromiminuit.Minuitwith the methodsiminuit.Minuit.validandiminuit.Minuit.accurate.See also
iminuit.Minuit.values,iminuit.Minuit.errors,iminuit.Minuit.merrors,iminuit.Minuit.covariance,iminuit.Minuit.fval,iminuit.Minuit.valid,iminuit.Minuit.accurate- property algorithm: str
Get algorithm that was used to compute the function minimum.
- property edm: float
Get Estimated Distance to Minimum.
Minuit uses this criterion to determine whether the fit converged. It depends on the gradient and the Hessian matrix. It measures how well the current second order expansion around the function minimum describes the function, by taking the difference between the predicted (based on gradient and Hessian) function value at the minimum and the actual value.
- property edm_goal: float
Get EDM threshold value for stopping the minimization.
The threshold is allowed to be violated by a factor of 10 in some situations.
- property errordef: float
Equal to the value of
iminuit.Minuit.errordefwhen Migrad ran.
- property fval: float
Get cost function value at the minimum.
- property has_accurate_covar: bool
Return whether the covariance matrix is accurate.
While Migrad runs, it computes an approximation to the current Hessian matrix. If the strategy is set to 0 or if the fit did not converge, the inverse of this approximation is returned instead of the inverse of the accurately computed Hessian matrix. This property returns False if the approximation has been returned instead of an accurate matrix computed by the Hesse method.
- property has_covariance: bool
Return whether a covariance matrix was computed at all.
This is false if the Simplex minimization algorithm was used instead of Migrad, in which no approximation to the Hessian is computed.
- property has_made_posdef_covar: bool
Return whether the matrix was forced to be positive definite.
While Migrad runs, it computes an approximation to the current Hessian matrix. It can happen that this approximation is not positive definite, but that is required to compute the next Newton step. Migrad then adds an appropriate diagonal matrix to enforce positive definiteness.
If the fit has converged successfully, this should always return False. If Minuit forced the matrix to be positive definite, the parameter uncertainties are false, see
has_posdef_covarfor more details.
- property has_parameters_at_limit: bool
Return whether any bounded parameter was fitted close to a bound.
The estimated error for the affected parameters is usually off. May be an indication to remove or loosen the limits on the affected parameter.
- property has_posdef_covar: bool
Return whether the Hessian matrix is positive definite.
This must be the case if the extremum is a minimum, otherwise it is a saddle point. If it returns False, the fitted result may be correct, but the reported uncertainties are false. This may affect some parameters or all of them. Possible causes:
Model contains redundanted parameters that are 100% correlated. Fix: remove the parameters that are 100% correlated.
Cost function is not computed in double precision. Fix: try adjusting
iminuit.Minuit.precisionor change the cost function to compute in double precision.Cost function is not analytical near the minimum. Fix: change the cost function to something analytical. Functions are not analytical if:
It does computations based on (pseudo)random numbers.
It contains vertical steps, for example from code like this:
if cond: return value1 else: return value2
- property has_reached_call_limit: bool
Return whether Migrad exceeded the allowed number of function calls.
Returns True true, the fit was stopped before convergence was reached; otherwise returns False.
- property has_valid_parameters: bool
Return whether parameters are valid.
This is the same as
is_validand only kept for backward compatibility.
- property hesse_failed: bool
Return whether the last call to Hesse failed.
- property is_above_max_edm: bool
Return whether the EDM value is below the convergence threshold.
Returns True, if the fit did not converge; otherwise returns False.
- property is_valid: bool
Return whether Migrad converged successfully.
For it to return True, the following conditions need to be fulfilled:
has_reached_call_limitis Falseis_above_max_edmis False
Note: The actual verdict is computed inside the Minuit2 C++ code, so we cannot guarantee that is_valid is exactly equivalent to these conditions.
- property nfcn: int
Get number of function calls so far.
- property ng2: int
Get number of g2 calls so far.
- property ngrad: int
Get number of gradient calls so far.
- property nhessian: int
Get number of hessian calls so far.
- property reduced_chi2: float
Get χ²/ndof of the fit.
This returns NaN if the cost function is unbinned, errordef is not 1, or if the cost function does not report the degrees of freedom.
- property time: float
Runtime of the last algorithm.
- class iminuit.util.FixedView(minuit: Any, ndim: int = 0)
Array-like view of whether parameters are fixed.
- to_dict() Dict[str, float]
Obtain dict representation.
- class iminuit.util.LimitView(minuit: Any)
Array-like view of parameter limits.
- to_dict() Dict[str, float]
Obtain dict representation.
- class iminuit.util.MError(number: int, name: str, lower: float, upper: float, is_valid: bool, lower_valid: bool, upper_valid: bool, at_lower_limit: bool, at_upper_limit: bool, at_lower_max_fcn: bool, at_upper_max_fcn: bool, lower_new_min: float, upper_new_min: float, nfcn: int, min: float)
Minos data object.
- number
Parameter index.
- Type:
int
- name
Parameter name.
- Type:
str
- lower
Lower error.
- Type:
float
- upper
Upper error.
- Type:
float
- is_valid
Whether Minos computation was successful.
- Type:
bool
- lower_valid
Whether downward scan was successful.
- Type:
bool
- upper_valid
Whether upward scan was successful.
- Type:
bool
- at_lower_limit
Whether scan reached lower limit.
- Type:
bool
- at_upper_limit
Whether scan reached upper limit.
- Type:
bool
- at_lower_max_fcn
Whether allowed number of function evaluations was exhausted.
- Type:
bool
- at_upper_max_fcn
Whether allowed number of function evaluations was exhausted.
- Type:
bool
- lower_new_min
Parameter value for new minimum, if one was found in downward scan.
- Type:
float
- upper_new_min
Parameter value for new minimum, if one was found in upward scan.
- Type:
float
- nfcn
Number of function calls.
- Type:
int
- min
Function value at the new minimum.
- Type:
float
- class iminuit.util.MErrors
Dict-like map from parameter name to Minos result object.
- clear() None. Remove all items from od.
- copy() a shallow copy of od
- fromkeys(value=None)
Create a new ordered dictionary with keys from iterable and values set to value.
- get(key, default=None, /)
Return the value for key if key is in the dictionary, else default.
- items() a set-like object providing a view on D's items
- keys() a set-like object providing a view on D's keys
- move_to_end(key, last=True)
Move an existing element to the end (or beginning if last is false).
Raise KeyError if the element does not exist.
- pop(key[, default]) v, remove specified key and return the corresponding value.
If the key is not found, return the default if given; otherwise, raise a KeyError.
- popitem(last=True)
Remove and return a (key, value) pair from the dictionary.
Pairs are returned in LIFO order if last is true or FIFO order if false.
- setdefault(key, default=None)
Insert key with a value of default if key is not in the dictionary.
Return the value for key if key is in the dictionary, else default.
- update([E, ]**F) None. Update D from dict/iterable E and F.
If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
- values() an object providing a view on D's values
- class iminuit.util.Param(number: int, name: str, value: float, error: float, merror: Tuple[float, float] | None, is_const: bool, is_fixed: bool, lower_limit: float | None, upper_limit: float | None)
Data object for a single Parameter.
- property has_limits
Query whether the parameter has an lower or upper limit.
- property has_lower_limit
Query whether parameter has a lower limit.
- property has_upper_limit
Query whether parameter has an upper limit.
- class iminuit.util.Params(iterable=(), /)
Tuple-like holder of parameter data objects.
- count(value, /)
Return number of occurrences of value.
- index(value, start=0, stop=9223372036854775807, /)
Return first index of value.
Raises ValueError if the value is not present.
- to_table() Tuple[List[List[str]], List[str]]
Convert parameter data to a tabular format.
The output is consumable by the external tabulate module.
Examples
>>> import tabulate as tab >>> from iminuit import Minuit >>> m = Minuit(lambda x, y: x ** 2 + (y / 2) ** 2 + 1, x=0, y=0) >>> m.fixed["x"] = True >>> m.migrad().minos() >>> tab.tabulate(*m.params.to_table()) pos name value error error- error+ limit- limit+ fixed ----- ------ ------- ------- -------- -------- -------- -------- ------- 0 x 0 0.1 yes 1 y 0 1.4 -1.0 1.0
- class iminuit.util.ValueView(minuit: Any, ndim: int = 0)
Array-like view of parameter values.
- to_dict() Dict[str, float]
Obtain dict representation.
- iminuit.util.describe(callable: Callable) List[str]
- iminuit.util.describe(callable: Callable, *, annotations: bool) Dict[str, Tuple[float, float] | None]
Attempt to extract the function argument names and annotations.
- Parameters:
callable (callable) – Callable whose parameter names should be extracted.
annotations (bool, optional) – Whether to also extract annotations. Default is false.
- Returns:
If annotate is False, return list of strings with the parameters names if successful and an empty list otherwise. If annotations is True, return a dict, which maps parameter names to annotations. For parameters without annotations, the dict maps to None.
- Return type:
list or dict
Notes
Parameter names are extracted with the following three methods, which are attempted in order. The first to succeed determines the result.
Using
obj._parameters, which is a dict that maps parameter names to parameter limits or None if the parameter has to limits. Users are encouraged to use this mechanism to provide signatures for objects that otherwise would not have a detectable signature. Example:def f(*args): # no signature x, y = args return (x - 2) ** 2 + (y - 3) ** 2 f._parameters = {"x": None, "y": (1, 4)}
Here, the first parameter is declared to have no limits (values from minus to plus infinity are allowed), while the second parameter is declared to have limits, it cannot be smaller than 1 or larger than 4.
Note: In the past, the
func_codeattribute was used for a similar purpose as_parameters. It is still supported for legacy code, but should not be used anymore in new code, since it does not support declaring parameter limits.If an objects has a
func_codeattribute, it is used to detect the parameters. Example:from iminuit.util import make_func_code def f(*args): # no signature x, y = args return (x - 2) ** 2 + (y - 3) ** 2 # deprecated, make_func_code will raise a warning f.func_code = make_func_code(("x", "y"))
Using
inspect.signature(). Theinspectmodule provides a general function to extract the signature of a Python callable. It works on most callables, including Functors like this:class MyLeastSquares: def __call__(self, a, b): ...
Limits are supported via annotations, using the Annotated type that was introduced in Python-3.9 and can be obtained from the external package typing_extensions in Python-3.8. In the following example, the second parameter has a lower limit at 0, because it must be positive:
from typing import Annotated def my_cost_function(a: float, b: Annotated[float, 0:]): ...
There are no standard annotations yet at the time of this writing. iminuit supports the annotations Gt, Ge, Lt, Le from the external package annotated-types, and interprets slice notation as limits.
Using the docstring. The docstring is textually parsed to detect the parameter names. This requires that a docstring is present which follows the Python standard formatting for function signatures. Here is a contrived example which is parsed correctly: fn(a, b: float, int c, d=1, e: float=2.2, double e=3).
Ambiguous cases with positional and keyword argument are handled in the following way:
def fcn(a, b, *args, **kwargs): ... # describe returns [a, b]; # *args and **kwargs are ignored def fcn(a, b, c=1): ... # describe returns [a, b, c]; # positional arguments with default values are detected
- iminuit.util.g2(fcn: Cost) CostVector | None
Return a callable which computes the diagonal of the Hessian of fcn or None.
- Parameters:
fcn (Cost) – Cost function which may provide a callable g2 function. How the g2 is detected is specified below in the Notes.
Notes
This function checks whether the following attributes exist: fcn.g2 and fcn.has_g2. If fcn.g2 exists and and satisfies the
iminuit.typing.CostVectorprotocol, it is returned unless fcn.has_g2 exists and is False. If no useable gradient is detected, None is returned.- Returns:
The gradient function or None
- Return type:
callable or None
- iminuit.util.gradient(fcn: Cost) CostVector | None
Return a callable which computes the gradient of fcn or None.
- Parameters:
fcn (Cost) – Cost function which may provide a callable gradient. How the gradient is detected is specified below in the Notes.
Notes
This function checks whether the following attributes exist: fcn.grad and fcn.has_grad. If fcn.grad exists and and satisfies the
iminuit.typing.CostVectorprotocol, it is returned unless fcn.has_grad exists and is False. If no useable gradient is detected, None is returned.- Returns:
The gradient function or None
- Return type:
callable or None
- iminuit.util.hessian(fcn: Cost) CostVector | None
Return a callable which computes the Hessian matrix of fcn or None.
- Parameters:
fcn (Cost) – Cost function which may provide a callable Hessian function. How the Hessian is detected is specified below in the Notes.
Notes
This function checks whether the following attributes exist: fcn.hessian and fcn.has_hessian. If fcn.hessian exists and satisfies the
iminuit.typing.CostVectorprotocol, it is returned unless fcn.has_grad exists and is False. If no useable gradient is detected, None is returned.- Returns:
The gradient function or None
- Return type:
callable or None
- iminuit.util.is_jupyter() bool
Return True if we are running in Jupyter.
- iminuit.util.is_module_available(module: str) bool
Return True if a module is available.
- iminuit.util.is_positive_definite(m: ArrayLike) bool
Return True if argument is a positive definite matrix.
This test is somewhat expensive, because we attempt a cholesky decomposition.
- Parameters:
m (array-like) – Matrix to be tested.
- Returns:
True if matrix is positive definite and False otherwise.
- Return type:
bool
- iminuit.util.make_func_code(*args: Any, **kwargs: Any) Any
make_func_code is deprecated: Use of
func_codeattribute to declare parameters is deprecated. Use_parametersinstead, which is a dict of parameter names to limits.
- iminuit.util.make_with_signature(callable: Callable, *varnames: str, **replacements: str) Callable
Return new callable with altered signature.
- Parameters:
callable – Original callable with positional arguments, whose names shall be changed.
*varnames (sequence of str) – Replace the first N argument names with these.
**replacements (mapping of str to str, optional) – Replace old argument name (key) with new argument name (value).
- Return type:
Callable with positional-only arguments.
- iminuit.util.merge_signatures(callables: Iterable[Callable], annotations: bool = False) Tuple[Any, List[List[int]]]
Merge signatures of callables with positional arguments.
This is best explained by an example:
def f(x, y, z): ... def g(x, p): ... parameters, mapping = merge_signatures(f, g) # parameters is ('x', 'y', 'z', 'p') # mapping is ([0, 1, 2], [0, 3])
- Parameters:
callables – Callables whose parameters can be extracted with
describe().annotations (bool, optional) – Whether to return the annotions. Default is False, for backward compatibility.
- Returns:
parameters is the tuple of the merged parameter names. mapping contains the mapping of parameters indices from the merged signature to the original signatures.
- Return type:
tuple(parameters, mapping)
- class iminuit.util.Matrix(parameters: Dict | Tuple)
Enhanced Numpy ndarray.
Works like a normal ndarray in computations, but also supports pretty printing in ipython and Jupyter notebooks. Elements can be accessed via indices or parameter names.
- correlation()
Compute and return correlation matrix.
If the matrix is already a correlation matrix, this effectively returns a copy of the original matrix.
- to_dict() Dict[Tuple[str, str], float]
Convert matrix to dict.
Since the matrix is symmetric, the dict only contains the upper triangular matrix.
- to_table() Tuple[List[List[str]], Tuple[str, ...]]
Convert matrix to tabular format.
The output is consumable by the external tabulate module.
Examples
>>> import tabulate as tab >>> from iminuit import Minuit >>> m = Minuit(lambda x, y: x ** 2 + y ** 2, x=1, y=2).migrad() >>> tab.tabulate(*m.covariance.to_table()) x y -- --- --- x 1 -0 y -0 4