Fitting RooFit-generated likelihoods
In this tutorial, we show how to create a negative log-likelihood function with the RooFit framework and minimize it with iminuit.
RooFit is a powerful fitting framework developed by CERN’s ROOT team. RooFit is very powerful and sophisticated, but there are a few reasons to use iminuit instead:
RooFit documention is extensive, but lacking in important places
RooFit interfaces are not Pythonic, they mimic the C++ interfaces (which are also dated)
Errors are difficult to understand and debug since RooFit is internally executing C++ code
You may experience segmentation faults when using RooFit from Python due to bugs in the ROOT Python layer (problems with handling life-times of dynamic C++ objects in Python correctly)
For these reasons, you may consider to transition to iminuit and its cost functions for your project. As a first step, you want to convince yourself that iminuit gives you the same fitting result as you get from RooFit.
[ ]:
import numpy as np
# ROOT is best installed via a conda virtual environment from conda-forge
import ROOT
from scipy.stats import truncnorm
from iminuit import Minuit
from iminuit.cost import UnbinnedNLL
Welcome to JupyROOT 6.26/10
[ ]:
# fix PRNG seed for RooFit random number generation
ROOT.RooRandom.randomGenerator().SetSeed(1)
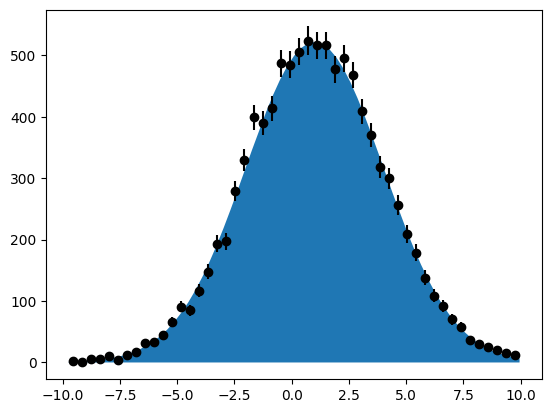
We generate a Gaussian with mean 1 and width 3 and draw 10000 data points from it.
[ ]:
x = ROOT.RooRealVar("x", "x", -10, 10)
mean = ROOT.RooRealVar("mean", "mean of gaussian", 1, -10, 10)
sigma = ROOT.RooRealVar("sigma", "width of gaussian", 3, 0.1, 10)
gauss = ROOT.RooGaussian("gauss", "gaussian PDF", x, mean, sigma)
data = gauss.generate({x}, 10000)
We now fit this Gaussian. We use the createNLL method and a simple wrapper function evaluate. Note that this simple wrapping function does not propagate the parameter names of the Gaussian to iminuit. A future version of iminuit will come with a builtin wrapper that will also propagate the names and limits.
[ ]:
nll = gauss.createNLL(data)
def evaluate(*args):
for par, arg in zip(nll.getVariables(), args):
par.setVal(arg)
# following RooMinimizerFcn.cxx
nll.setHideOffset(False)
r = nll.getVal()
nll.setHideOffset(True)
return r
evaluate.errordef = Minuit.LIKELIHOOD
m = Minuit(evaluate, *[p.getVal() for p in nll.getVariables()])
m.migrad()
| Migrad | ||||
|---|---|---|---|---|
| FCN = 2.514e+04 | Nfcn = 31 | |||
| EDM = 2.72e-08 (Goal: 0.0001) | ||||
| Valid Minimum | No Parameters at limit | |||
| Below EDM threshold (goal x 10) | Below call limit | |||
| Covariance | Hesse ok | Accurate | Pos. def. | Not forced |
| Name | Value | Hesse Error | Minos Error- | Minos Error+ | Limit- | Limit+ | Fixed | |
|---|---|---|---|---|---|---|---|---|
| 0 | x0 | 1.003 | 0.030 | |||||
| 1 | x1 | 3.017 | 0.022 |
| x0 | x1 | |
|---|---|---|
| x0 | 0.000926 | 0 (0.030) |
| x1 | 0 (0.030) | 0.000497 |
Let’s compare this to fitting directly with the fitTo method.
[ ]:
gauss.fitTo(data);
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 mean 1.00653e+00 2.00000e+00 -1.00000e+01 1.00000e+01
2 sigma 3.01930e+00 9.90000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=25136.7 FROM MIGRAD STATUS=INITIATE 10 CALLS 11 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mean 1.00653e+00 2.00000e+00 2.02444e-01 3.46428e+01
2 sigma 3.01930e+00 9.90000e-01 2.22272e-01 2.14205e+01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=25136.7 FROM MIGRAD STATUS=CONVERGED 25 CALLS 26 TOTAL
EDM=1.96964e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mean 1.00330e+00 3.04253e-02 3.34944e-04 1.02604e+00
2 sigma 3.01694e+00 2.22842e-02 5.41347e-04 6.16930e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
9.257e-04 2.032e-05
2.032e-05 4.966e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.02997 1.000 0.030
2 0.02997 0.030 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=25136.7 FROM HESSE STATUS=OK 10 CALLS 36 TOTAL
EDM=1.96993e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 mean 1.00330e+00 3.04246e-02 6.69888e-05 1.00499e-01
2 sigma 3.01694e+00 2.22838e-02 1.08269e-04 -4.23243e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
9.257e-04 1.984e-05
1.984e-05 4.966e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.02926 1.000 0.029
2 0.02926 0.029 1.000
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
The results are in agreement, because the results of a fit cannot depend on the minimizer. Technically, RooFit uses a different minimizer than iminuit by default. Unless you change some options, RooFit uses the original MINUIT Fortran implementation translated to C, while iminuit uses the rewritten Minuit2 C++ library.
Just doing the fitting with iminuit does not offer you a lot of advantages. Eventually, you want to switch completely. The equivalent of this exercise in pure Python is the following.
[ ]:
xrange = (-10.0, 10.0)
rng = np.random.default_rng(1)
x = rng.normal(1, 3, size=10000)
x = x[(xrange[0] < x) & (x < xrange[1])]
def model(x, mu, sigma):
zrange = np.subtract(xrange, mu) / sigma
return truncnorm.pdf(x, *zrange, mu, sigma)
# better use numba_stats.truncnorm, which is simpler to use and faster
#
# from numba_stats import truncnorm
#
# def model(x, mu, sigma):
# return truncnorm.pdf(x, *xrange, mu, sigma)
nll = UnbinnedNLL(x, model)
m = Minuit(nll, 1, 3)
m.migrad()
| Migrad | ||||
|---|---|---|---|---|
| FCN = 4.998e+04 | Nfcn = 29 | |||
| EDM = 3e-06 (Goal: 0.0002) | ||||
| Valid Minimum | No Parameters at limit | |||
| Below EDM threshold (goal x 10) | Below call limit | |||
| Covariance | Hesse ok | Accurate | Pos. def. | Not forced |
| Name | Value | Hesse Error | Minos Error- | Minos Error+ | Limit- | Limit+ | Fixed | |
|---|---|---|---|---|---|---|---|---|
| 0 | mu | 0.96 | 0.03 | |||||
| 1 | sigma | 2.985 | 0.022 |
| mu | sigma | |
|---|---|---|
| mu | 0.000906 | 0 (0.027) |
| sigma | 0 (0.027) | 0.000483 |
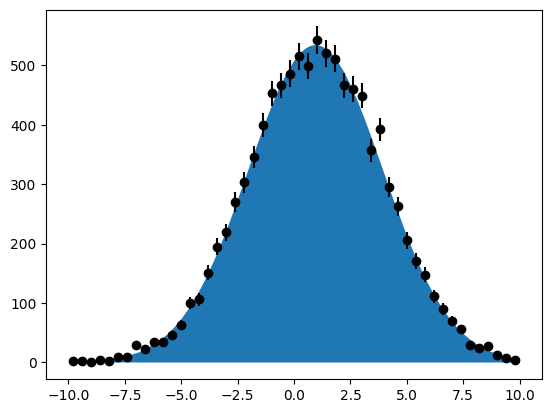
We do not get the exact same fitted values as before, since the data sample is different from the one generated by RooFit.
To get the exact same result, we need to convert the variable data which has the type RooDataSet into a numpy array. The ROOT Python layer offers the method to_numpy for this purpose.
[ ]:
x = data.to_numpy()["x"]
nll = UnbinnedNLL(x, model)
m = Minuit(nll, 1, 3)
m.migrad()
| Migrad | ||||
|---|---|---|---|---|
| FCN = 5.027e+04 | Nfcn = 31 | |||
| EDM = 5.43e-08 (Goal: 0.0002) | ||||
| Valid Minimum | No Parameters at limit | |||
| Below EDM threshold (goal x 10) | Below call limit | |||
| Covariance | Hesse ok | Accurate | Pos. def. | Not forced |
| Name | Value | Hesse Error | Minos Error- | Minos Error+ | Limit- | Limit+ | Fixed | |
|---|---|---|---|---|---|---|---|---|
| 0 | mu | 1.003 | 0.030 | |||||
| 1 | sigma | 3.017 | 0.022 |
| mu | sigma | |
|---|---|---|
| mu | 0.000926 | 0 (0.030) |
| sigma | 0 (0.030) | 0.000497 |